算法兴趣培养计划第三日

问题描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

输入格式

输入只有一行，包含一个正整数 n（1 <= N <= 45），表示总阶梯数。

第一题

你需要求出 n=5 时答案并阐述解决本题的思路

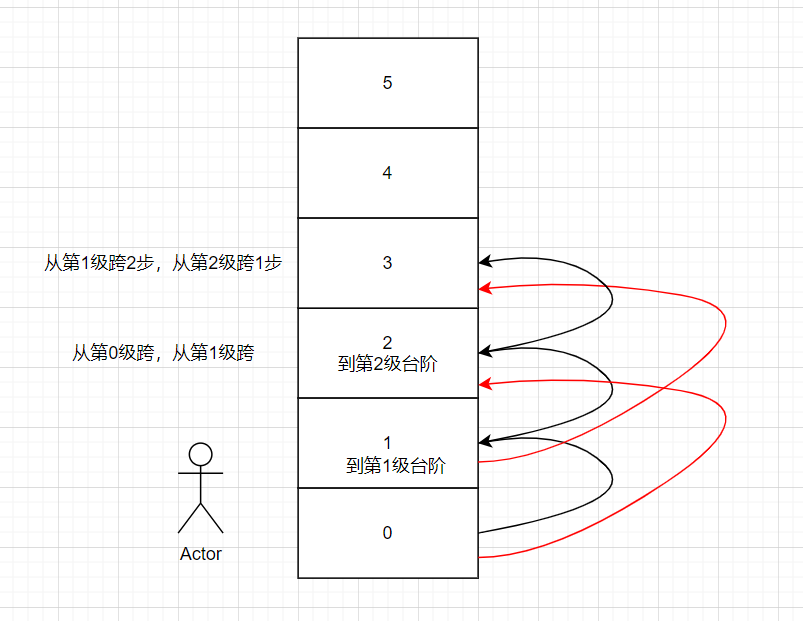
到第 1 级只有 1 种方法，就是从第 0 级一步到达第 1 级。到第二级有 2 种方法，一种是从第 0 级一步到达第 2 级，另一种是从第 1 级一步到达第 2 级。到第三级有 3 种方法，一种是从第 0 级一步到达第 3 级，一种是从第 1 级一步到达第 3 级，还有一种是从第 2 级一步到达第 3 级。

思路

假设我们一共要跳 5 级台阶

如果最后一步爬了 1 个台阶，那么我们得先爬到 4，要解决的问题缩小成：从 0 爬到 4 有多少种不同的方法。
如果最后一步爬了 2 个台阶，那么我们得先爬到 3 ，要解决的问题缩小成：从 0 爬到 3 有多少种不同的方法。
跳 4 级台阶的方法数 = 跳 3 级台阶的方法数 + 跳 2 级台阶的方法数

对于 n = 5，计算过程如下：

f(3) = f(2) + f(1) = 2 + 1 = 3f(4) = f(3) + f(2) = 3 + 2 = 5f(5) = f(4) + f(3) = 5 + 3 = 8 因此，n = 5 时，答案是 8。最后可以得出答案为 8

推广

设跳上 $n$ 级台阶有 $f (n)$ 种跳法。在所有跳法中，最后一步只有两种情况：跳上 1 级或 2 级台阶。

当为 1 级台阶：剩 $n - 1$ 个台阶，此情况共有 $f (n - 1)$ 种跳法。当为 2 级台阶：剩 $n - 2$ 个台阶，此情况共有 $f (n - 2)$ 种跳法。

解法

典型错误

#include <stdio.h>
int f(int n)
{
    if (n == 1)
        return 1;
    else if (n == 2)
        return 2;
    else
        return f(n - 1) + f(n - 2);
}

int main()
{
    int n;
    scanf("%d", &n);
    printf("%d", f(n));
    return 0;
}

这里可以看一下为什么这个代码是错误的，这个代码的时间复杂度是指数级别的，这个代码的时间复杂度是 $O (2^{n})$

打表。。。。。。。。。

#include <stdio.h>
int main(){
    int n;
    scanf("%d", &n);
    switch(n){
    case 1: result = 1; break;
    case 2: result = 2; break;
    case 3: result = 3; break;
    case 4: result = 5; break;
    case 5: result = 8; break;
    case 6: result = 13; break;
    case 7: result = 21; break;
    case 8: result = 34; break;
    case 9: result = 55; break;
    case 10: result = 89; break;
    case 11: result = 144; break;
    case 12: result = 233; break;
    case 13: result = 377; break;
    case 14: result = 610; break;
    case 15: result = 987; break;
    case 16: result = 1597; break;
    case 17: result = 2584; break;
    case 18: result = 4181; break;
    case 19: result = 6765; break;
    case 20: result = 10946; break;
    case 21: result = 17711; break;
    case 22: result = 28657; break;
    case 23: result = 46368; break;
    case 24: result = 75025; break;
    case 25: result = 121393; break;
    case 26: result = 196418; break;
    case 27: result = 317811; break;
    case 28: result = 514229; break;
    case 29: result = 832040; break;
    case 30: result = 1346269; break;
    case 31: result = 2178309; break;
    case 32: result = 3524578; break;
    case 33: result = 5702887; break;
    case 34: result = 9227465; break;
    case 35: result = 14930352; break;
    case 36: result = 24157817; break;
    case 37: result = 39088169; break;
    case 38: result = 63245986; break;
    case 39: result = 102334155; break;
    case 40: result = 165580141; break;
    case 41: result = 267914296; break;
    case 42: result = 433494437; break;
    case 43: result = 701408733; break;
    case 44: result = 1134903170; break;
    case 45: result = 1836311903; break;
    }
    printf("%d\n", result);
    return 0;
}

递推

#include <stdio.h>
int main(){
    int n;
    scanf("%d", &n);
    int level1 = 1, level2 = 2, result = 0;
    if(n == 1){
        result = 1;
    }else if(n == 2){
        result = 2;
    }else{
        for(int i = 3; i <= n; i++){
            result = level1 + level2;
            level1 = level2;
            level2 = result;
        }
    }
    printf("%d\n", result);
    return 0;
}

使用下面这种写法也可以

#include <stdio.h>
int main(){
    int n;
    scanf("%d", &n);
    int dp[50];
    dp[1] = 1;
    dp[2] = 2;
    for(int i = 3; i <= n; i++){
        dp[i] = dp[i-1] + dp[i-2];
    }
    printf("%d\n", dp[n]);
    return 0;
}

希望不要出现非预期的现象。。。。。。。。

批改后出现了拓展的解答

#include<stdio.h>
long long int arr[5003][2000];  //二维数组每行存储一个数字，数组中每个数字代表一个位数
int main(void){
    int n,len=1;
    for (int i=0;i<5003;i++){   //初始化数组
        for (int j=0;j<2000;j++){
            arr[i][j]=0;
        }
    }
    scanf("%d", &n);
    arr[0][0]=0;   //初始化数据
    arr[1][0]=1;
    arr[2][0]=2;
    for (int i = 3;i <= n; i++){
        for (int j = 0;j < len; j++){
            arr[i][j]=arr[i-1][j]+arr[i-2][j];    //计算前两个数每个对应位的数字相加
        }
        for (int j=0;j<len;j++){
            if (arr[i][j] > 9){     //进位，保证每个数组元素都小于10
                arr[i][j + 1 ] += arr[i][j] / 10;
                arr[i][j] %= 10;
            }
        }
        if (arr[i][len]>0) len++;    //处理进位
        }
    for (int i = len-1;i >= 0; i--){
        printf("%lld",arr[n][i]);
    }
    return 0;
}

来解释一下他干了什么事情来看这样的整数加法

   1 2 3 4 5 6
+  1 2 3 4 5 8
-------------
   2 4 6 9 1 4

这里我 6+8 的时候得出了 14，这个时候就需要进位，进位后的结果是 4，然后把 1 加到下一个数上，这样就得到了结果

公式的推导

斐波那契数列的定义是：

$F_{1} = 1$
$F_{2} = 2$
对于 $n \geq 3$ ， $F_{n} = F_{n - 1} + F_{n - 2}$

1. 假设解的形式

假设递推关系式的解可以表示为指数形式：

F_{n} = r^{n}

将其代入递推公式 $F_{n} = F_{n - 1} + F_{n - 2}$ 中：

r^{n} = r^{n - 1} + r^{n - 2}

两边同除以 $r^{n - 2}$ ，得到：

r^{2} = r + 1

特征方程：

r^{2} - r - 1 = 0

利用求根公式，我们可以求出 $r$ 的两个根：

r_{1} = \frac{1 + \sqrt{5}}{2}, r_{2} = \frac{1 - \sqrt{5}}{2}

2. 通解

特征方程的通解是这两个根的线性组合，因此斐波那契数列的通项公式可以表示为：

F_{n} = A r_{1}^{n} + B r_{2}^{n}

其中， $A$ 和 $B$ 是待定的常数。

3. 利用初始条件求 $A$ 和 $B$

我们现在用已知的初始条件 $F_{1} = 1$ 和 $F_{2} = 2$ 来确定 $A$ 和 $B$ 。

对于 $n = 1$ ：
$F_{1} = A r_{1} + B r_{2} = 1$
对于 $n = 2$ ：
$F_{2} = A r_{1}^{2} + B r_{2}^{2} = 2$

接下来我们求出 $r_{1}^{2}$ 和 $r_{2}^{2}$ ：

r_{1}^{2} = r_{1} + 1 = \frac{1 + \sqrt{5}}{2} + 1 = \frac{3 + \sqrt{5}}{2}

r_{2}^{2} = r_{2} + 1 = \frac{1 - \sqrt{5}}{2} + 1 = \frac{3 - \sqrt{5}}{2}

因此，第二个方程变为：

A \frac{3 + \sqrt{5}}{2} + B \frac{3 - \sqrt{5}}{2} = 2

现在我们有如下的方程组：

A r_{1} + B r_{2} = 1

A \frac{3 + \sqrt{5}}{2} + B \frac{3 - \sqrt{5}}{2} = 2

解这个方程组可以得到 $A$ 和 $B$ 的值。解出后，代入通解公式，我们就得到了斐波那契数列的通项公式。

通过进一步计算，我们可以发现：

A = \frac{2}{\sqrt{5}}, B = - \frac{1}{\sqrt{5}}

最终的通项公式为：

F_{n} = \frac{2}{\sqrt{5}} {(\frac{1 + \sqrt{5}}{2})}^{n} - \frac{1}{\sqrt{5}} {(\frac{1 - \sqrt{5}}{2})}^{n}

代码实现

#include <bits/stdc++.h>
using namespace std;

using i64 = long long;

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);

    int n;
    cin >> n;
    int res = floor((pow((1 + sqrt(5)) / 2, n + 1) - (pow((1 - sqrt(5)) / 2, n + 1))) / sqrt(5));
    cout << res << '\n';
    return 0;
}

样例答案

95 昏

这道题可以用递归算法来思考，每次可以爬 1 或 2 个台阶，说明每次操作有两种方案可以执行，如果说爬n阶楼梯用的方法是f(n)种，可以得到递推公式f(n)=f(n-1)+f(n-2)。在找到递归的终止条件就行了，终止条件为f(1)=1,f(2)=2。这样就能实现递归算法。

int fun(int x)
{
 if (x == 1)
  return 1;
 else if (x == 2)
  return 2;
 return fun(x - 1) + fun(x - 2);
}
但是当n较大时会运行超时，因此我查询了一些优化递归的方法：记忆递归

int arr[46] = { 0 };
int fun(int x)
{
 if (x == 1)
  return 1;
 else if (x == 2)
  return 2;
 else if (arr[x] != 0)
  return arr[x];
 return arr[x] = fun(x - 1) + fun(x - 2);
}
将已经计算出的结果存储起来，使得计算机在递归到深层时不用重复计算，极大减少了递归的时间。

90 昏

利用递推。

定义一个长度为5的数组装到达1-5层的方法数，

arr[1]=1,arr[2]=2
利用arr[i]=arr[i-1]+arr[i-2]这一递推公式和循环解题。

杂谈

javascript

function fn(n) {
  let last1 = 1,
    last2 = 1,
    temp;
  for (let i = 3; i <= n; i++) {
    temp = last1 + last2;
    last1 = last2;
    last2 = temp;
  }
  return last2;
}
console.log(fn(5));

一道轻松愉快的排列组合问题。

呃，考虑到这个不明所以的题目背景……先輩你是不是住五楼啊？

分个类，循个环，走五次一步（5C0），走三次一步一次两步（4C1）……然后你懂的，排列一下并求和（SUM((5-i)C(i)))。

什么，你说你说她的复杂度有点丑陋？呃……

好吧，我承认这并不是一道轻松愉快的排列组合问题。

…………

…………

…………

小子，你不会是个斐波那契数列吧。

设我们有f(n)种方法爬到楼顶，让我们来转移一下状态（应该叫这个吧），假设我们还有一步就要爬完这该死的楼梯了，那么显然，这个时候我们所在的劫数n'为n-1或n-2，前面忘了，中间忘了，后面忘了，易得

f(n)=f(n-1)+f(n-2)

小子，你绝对是个斐波那契数列吧？

先回答一下问题吧，免得又忘了，f(5)=8。

接下来就是……因该不会有人想看C语言求解斐波那契数列的思路吧？不会吧？不会吧？

Q.E.D.



好了，那么以上内容就是就是我在思考这道题时的全部思路了，包括那句“仙贝你是不是住五楼啊”。

当然，上面那句也是包括在内的。

当然，上面那句也是包括在内的。

当然，上面那句也是包括在内的。

…………

太好了，你循环条件炸了。

算法兴趣培养计划第三日 ​

问题描述 ​

输入格式 ​

第一题 ​

思路 ​

推广 ​

解法 ​

递推 ​

公式的推导 ​

1. 假设解的形式 ​

2. 通解 ​

3. 利用初始条件求 A 和 B ​

代码实现 ​

样例答案 ​

杂谈 ​